5 Comparing two curves

In this chapter, we’ll look into how, when and why to use the log rank test to compare stratified (grouped) survival curves to one another.

5.1 Libraries and functions

Click to expand

R
Python

# load the required packages for fitting & visualising
library(tidyverse)
library(survival)
library(survminer)

import numpy as np
import pandas as pd
from lifelines import *
import matplotlib.pyplot as plt

5.2 The log-rank (Mantel-Cox) test

We use this test in situations where we have a single categorical predictor in our dataset, and would like to find out whether two survival curves are significantly different from each other.

You might find it useful to think of the log-rank test as an analogue of a two-sample t-test, but for time-to-event data specifically.

The log-rank test is a null hypothesis significance test:

Our null hypothesis is that our two groups don’t differ in how likely they are to experience the event over time
Or, in other words: in the underlying population, the true survival curves are identical
So, if our p-value falls under the significance threshold, our data are very unlikely to have occurred just by chance, giving some evidence that a difference does exist

5.3 Assumptions of a log-rank test

Like all statistical tests, before we jump in and start calculating things, we need to consider some key statistical assumptions first.

If these aren’t met, the log-rank test won’t actually help us answer our research question.

5.3.1 Assumption 1: Independent observations

An “observation” = a unique row in the raw dataset, representing a unique individual in the study.

“Independent” means that none of the individuals are affected by any other individuals in the study, or artificially similar to them.

Common sources of non-independence would include:

Repeated measures (recording multiple rows/events of interest per individual)
Matched/paired designs
Natural “clusters” or “nesting”, e.g.,: patients within hospitals, or students within schools
Genetic relatedness, e.g., using animals from the same litter

Checking for independence

You might find some people online telling you about various quantitative tests for independence. I’m not going to do that, because the only reliable check for independence is a good understanding of your experimental design.

If you can think of any ways of grouping together the rows of your dataset, then that’s an indication that you have some dependency.

What if independence is violated?

You may need to consider something like a mixed effects Cox regression model. This is a combination of Cox regression (which we talk about later in this course) and mixed effects modelling (which needs a whole course all of its own).

5.3.2 Assumption 2: Non-informative censoring

The likelihood of censoring should not be related to the likelihood of experiencing the event of interest.

Phrased another way: the individuals who are censored are assumed to have had the same underlying time-to-event distribution as those who weren’t censored, if they had remained in the study.

Checking for non-informative censoring

The most obvious clue will be unequal rates of censoring between groups. This is a sign that censoring is not happening at random.

You will also need to consider your experimental design carefully.

What if censoring is informative?

You could consider a competing risks model.

5.3.3 Desirable: Proportional hazards

The hazard ratio - i.e., the increased risk of experiencing the event in group 1 versus group 2 - should ideally stay consistent over time.

In our hospital_stays dataset, proportional hazards would mean that if non-surgical patients are 2x more likely than surgical patients to be discharged on day 3, they would also be 2x more likely to get discharged on day 30 (and every day in between).

Checking for proportional hazards

There a handful of methods available to you:

Inspecting the Kaplan-Meier curves; if they cross over, that’s a bad sign
Creating log-log plots; you want the lines to be roughly parallel
Checking the Schoenfeld residuals

We’ll unpack some of these methods in more detail in later chapters when we look at Cox regression, where propotional hazards is more of a formal assumption.

What if hazards aren’t proportional?

The log-rank test becomes less powerful or sensitive (less likely to detect true differences).

It’s still valid, however. Remember that proportional hazards aren’t a formal assumption of the log-rank test.

5.4 Running a log-rank test

To practice implementing the test, let’s return to the hospital_stays dataset, which we plotted survival curves for in the last chapter.

Specifically, let’s focus on the sex and surgery predictors from the dataset.

R
Python

hospital_stays <- read_csv("data/hospital_stays.csv")

Rows: 200 Columns: 6
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
dbl (6): time, discharged, age, sex, surgery, weekend_admission

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

head(hospital_stays)

# A tibble: 6 × 6
   time discharged   age   sex surgery weekend_admission
  <dbl>      <dbl> <dbl> <dbl>   <dbl>             <dbl>
1   5            1    43     1       0                 0
2   0.5          1    48     0       0                 0
3  19            1    77     0       0                 0
4   4.5          1    50     0       0                 0
5   7            1    79     1       0                 1
6   1            1    73     1       0                 0

hospital_stays = pd.read_csv("data/hospital_stays.csv")

hospital_stays.head()

   time  discharged  age  sex  surgery  weekend_admission
0   5.0           1   43    1        0                  0
1   0.5           1   48    0        0                  0
2  19.0           1   77    0        0                  0
3   4.5           1   50    0        0                  0
4   7.0           1   79    1        0                  1

Log-rank test by surgery

When we stratified by surgery in the previous chapter, we got curves that looked like this:

R
Python

Warning in geom_segment(aes(x = 0, y = max(y2), xend = max(x1), yend = max(y2)), : All aesthetics have length 1, but the data has 2 rows.
ℹ Please consider using `annotate()` or provide this layer with data containing
  a single row.
All aesthetics have length 1, but the data has 2 rows.
ℹ Please consider using `annotate()` or provide this layer with data containing
  a single row.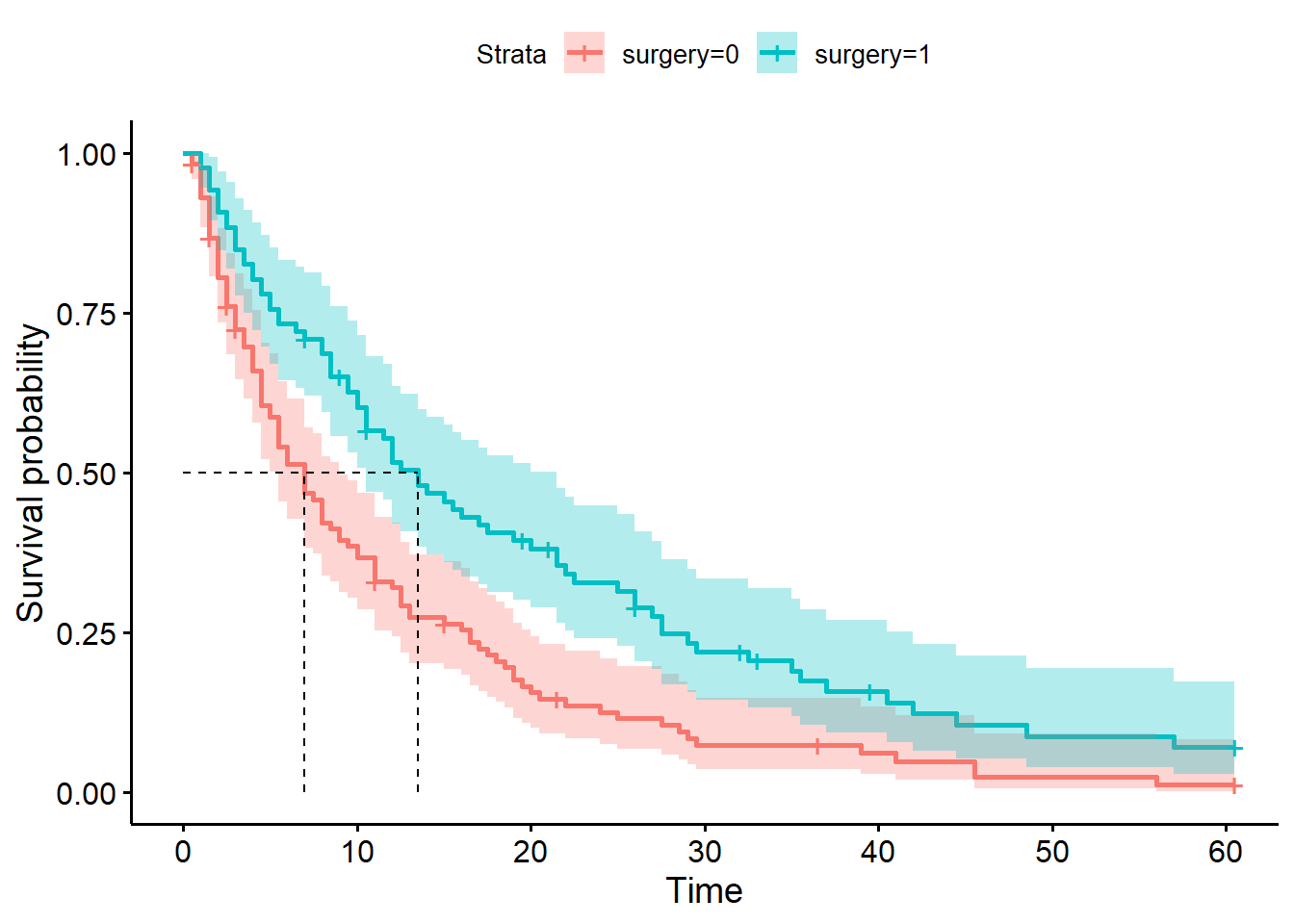

<lifelines.KaplanMeierFitter:"Surgical patients", fitted with 86 total observations, 13 right-censored observations>

<lifelines.KaplanMeierFitter:"Non-surgical patients", fitted with 114 total observations, 9 right-censored observations>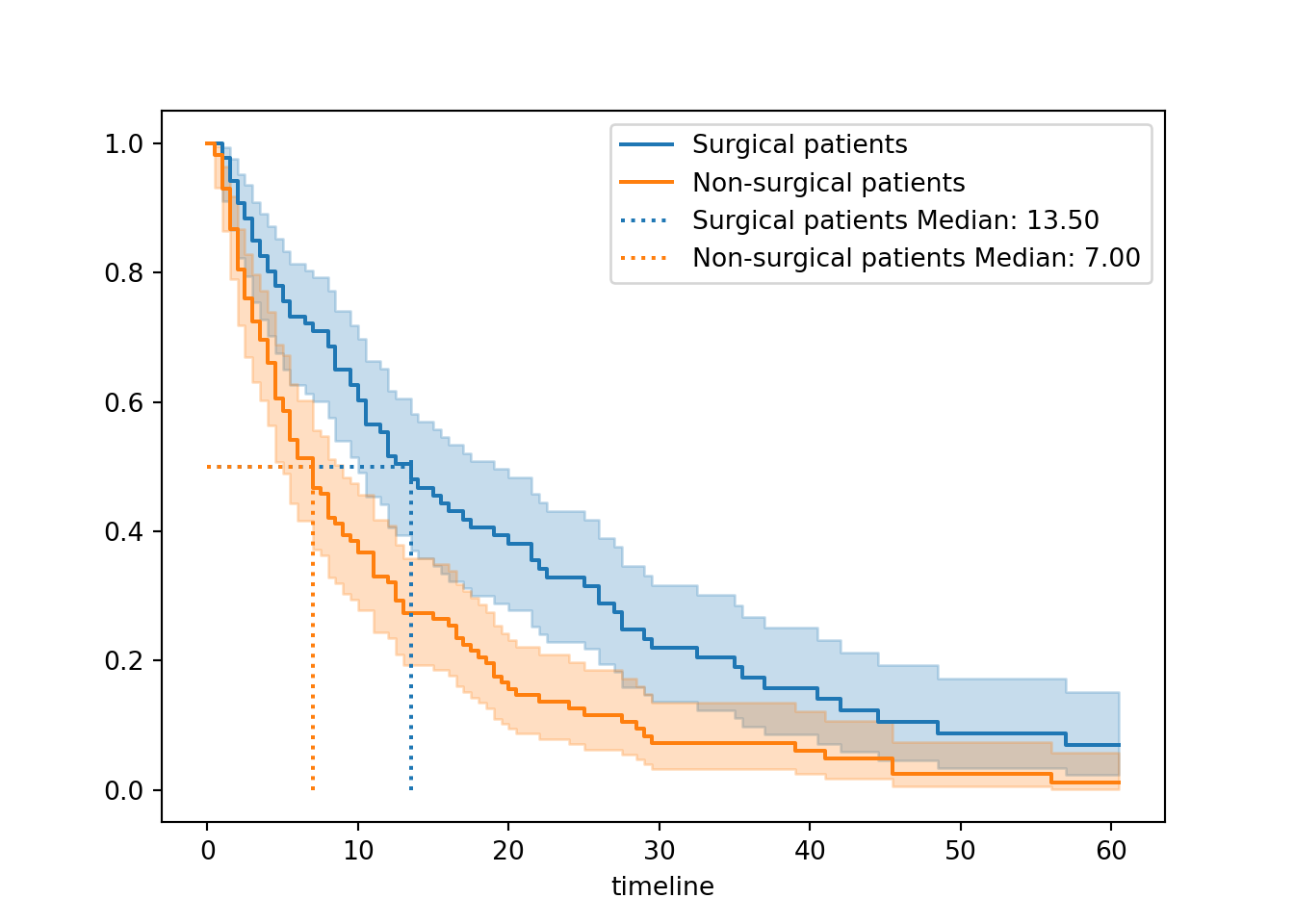

We determined that the median survival times for surgical (13.5 days) and non-surgical (7 days) patients were different. This indicates that surgical patients spend longer in hospital on average.

Now, let’s add a p-value to our weight of evidence, to see whether that difference is significant.

R
Python

In the survival package, this process is as simple as changing the function from survfit to survdiff.

None of the rest of the syntax changes. We still use a survival object Surv(time, discharged) as our response, and the ~ surgery formula to make our predictor variable clear.

survdiff(Surv(time, discharged) ~ surgery, data = hospital_stays)

Call:
survdiff(formula = Surv(time, discharged) ~ surgery, data = hospital_stays)

            N Observed Expected (O-E)^2/E (O-E)^2/V
surgery=0 114      105     81.4      6.85      13.4
surgery=1  86       73     96.6      5.77      13.4

 Chisq= 13.4  on 1 degrees of freedom, p= 3e-04

In the output, alongside the statistic and p-value, we are shown:

the n sample size in each group
the observed number of events (discharges from hospital) in each group
what the expected number of events would be, if there were no effect of surgery

There is a dedicated logrank_test function in the lifelines package.

We have to provide the following arguments:

The set of times T for the surgery = 1 group
The set of times T for the surgery = 0 group
The events (versus censoring) E for the surgery = 1 group
The events E for the surgery = 0 group

from lifelines.statistics import logrank_test

T = hospital_stays["time"]
E = hospital_stays["discharged"]

# Subset of the dataset that received surgery
surg = (hospital_stays["surgery"] == 1)

# Run the log-rank test
results = logrank_test(T[surg], T[~surg], E[surg], E[~surg])

results.print_summary()

<lifelines.StatisticalResult: logrank_test>
               t_0 = -1
 null_distribution = chi squared
degrees_of_freedom = 1
         test_name = logrank_test

---
 test_statistic      p  -log2(p)
          13.35 <0.005     11.92

You can access the exact p-value with results.p_value.

A chi-square (\(\chi^2\)) statistic has been calculated to summarise the difference between the two groups.

The associated p-value, in this case, tells us that the likelihood of observing two curves that are this (or more) different from each other, if surgery really had no effect on time-to-discharge in the hospital, is very low.

This is additional evidence for us that surgery probably does affect how quickly a patient can expect to be discharged.

For a final step, let’s add those p-values onto our plot:

R
Python

There are two additional arguments in ggsurvplot that you can make use of.

The pval argument tells the function to compute and add a p-value. The pval.method argument adds a text label to clarify what type of test was performed to get the p-value.

ggsurvplot(hosp_curve_surgery,
           conf.int = TRUE,
           surv.median.line = "hv",
           pval = TRUE, pval.method = TRUE)

Warning in geom_segment(aes(x = 0, y = max(y2), xend = max(x1), yend = max(y2)), : All aesthetics have length 1, but the data has 2 rows.
ℹ Please consider using `annotate()` or provide this layer with data containing
  a single row.
All aesthetics have length 1, but the data has 2 rows.
ℹ Please consider using `annotate()` or provide this layer with data containing
  a single row.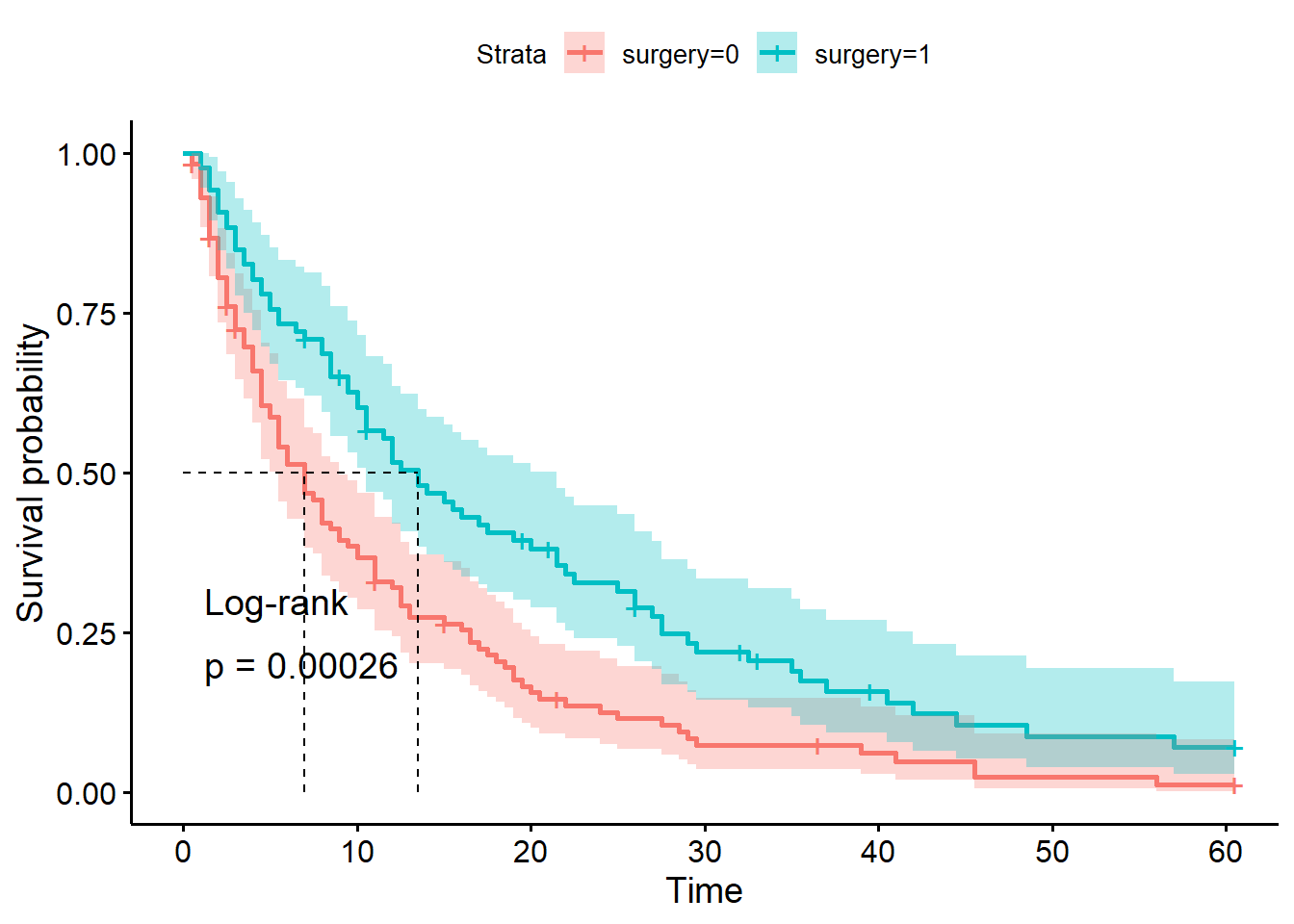

You have to add the p-value manually in lifelines.

First, save the p-value from the results output of the log-rank test. Then, annotate the plot with text.

You might need to adjust the x/y positions, depending on the exact shape of your curve(s).

# Kaplan Meier fit for surgical data subset
surg_hosp = KaplanMeierFitter()
surg_hosp.fit(T[surg], event_observed=E[surg], label="Surgical patients")

<lifelines.KaplanMeierFitter:"Surgical patients", fitted with 86 total observations, 13 right-censored observations>

# Kaplan Meier fit for non-surgical data subset
ns_hosp = KaplanMeierFitter()
ns_hosp.fit(T[~surg], event_observed=E[~surg], label="Non-surgical patients")

<lifelines.KaplanMeierFitter:"Non-surgical patients", fitted with 114 total observations, 9 right-censored observations>

# Initialise a plot to capture both of the curves
plt.clf()
fig, ax = plt.subplots()

# Add the two curves, one at a time
surg_hosp.plot_survival_function(ax = ax)
ns_hosp.plot_survival_function(ax = ax)

# Add the median markers for both curves
add_median_markers([surg_hosp, ns_hosp], ax = ax)

# Add the p-value
pval = results.p_value
ax.text(0.6, 0.6, f"Log-rank p = {pval:.3g}", transform=ax.transAxes)

plt.show()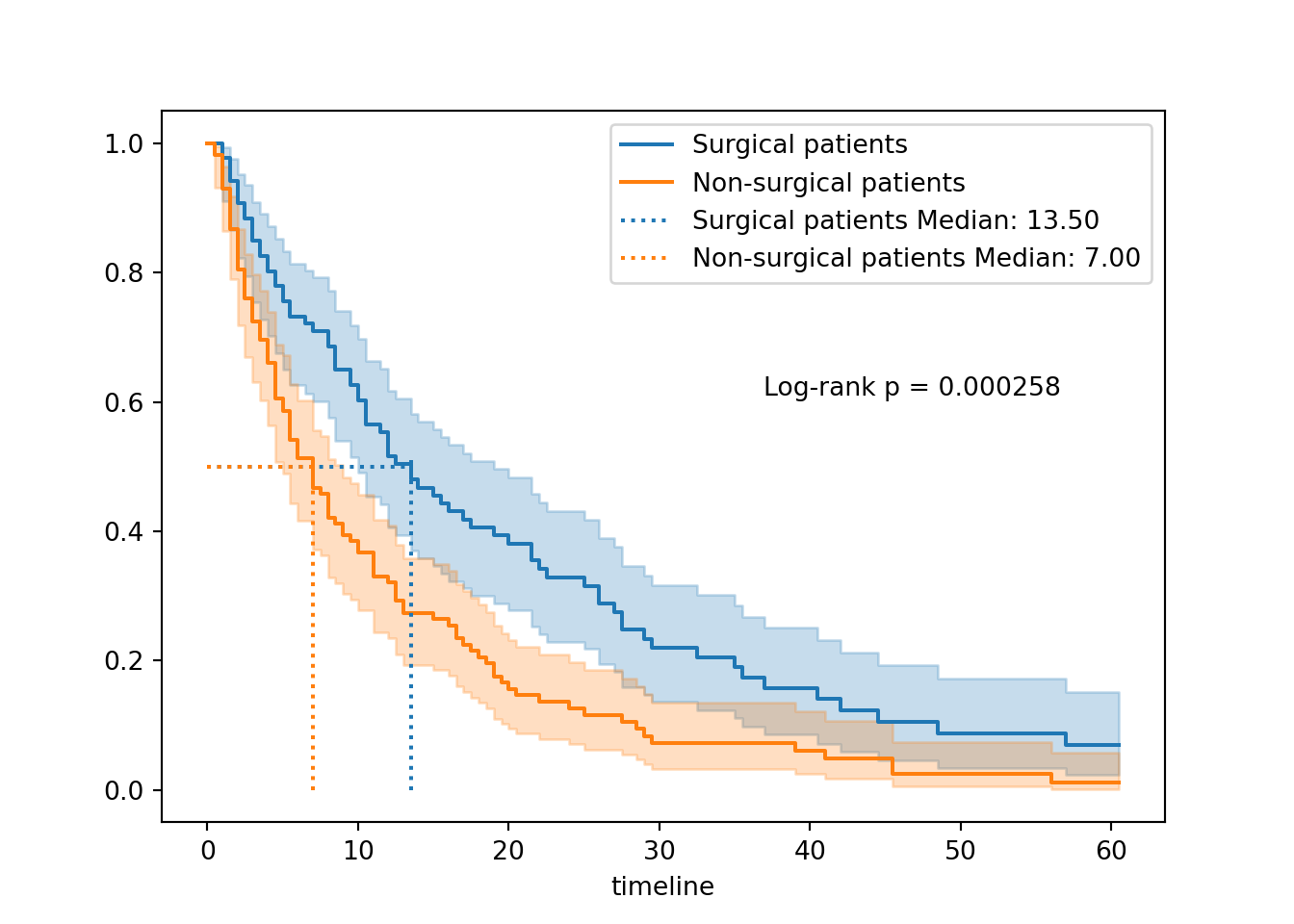

How is the log-rank statistic calculated?

Observed vs expected for each time point

Log-rank test by sex

In contrast, let’s run a log-rank test for a predictor variable where we didn’t see much visual difference in the curves: biological sex of the patient.

R
Python

survdiff(Surv(time, discharged) ~ sex, data = hospital_stays)

Call:
survdiff(formula = Surv(time, discharged) ~ sex, data = hospital_stays)

        N Observed Expected (O-E)^2/E (O-E)^2/V
sex=0  92       84       77     0.638      1.17
sex=1 108       94      101     0.486      1.17

 Chisq= 1.2  on 1 degrees of freedom, p= 0.3

# Subset of the dataset that are female
fem = (hospital_stays["sex"] == 0)

# Run the log-rank test
results = logrank_test(T[fem], T[~fem], E[fem], E[~fem])

results.print_summary()

<lifelines.StatisticalResult: logrank_test>
               t_0 = -1
 null_distribution = chi squared
degrees_of_freedom = 1
         test_name = logrank_test

---
 test_statistic    p  -log2(p)
           1.17 0.28      1.84

We see now that the chi-square statistic is much smaller, and the p-value much larger.

This suggests that the likelihood of seeing curves with this much difference (or greater), if there really was no difference between male and female patients, is actually quite high.

In other words: the small difference we’re observing is quite likely to have happened by chance.

Last but not least, let’s visualise the curves to help us contexualise the p-value a little better:

R
Python

hosp_curve_sex <- survfit(Surv(time, discharged) ~ sex, data = hospital_stays)

ggsurvplot(hosp_curve_sex,
           conf.int = TRUE,
           surv.median.line = "hv",
           pval = TRUE, pval.method = TRUE)

Warning in geom_segment(aes(x = 0, y = max(y2), xend = max(x1), yend = max(y2)), : All aesthetics have length 1, but the data has 2 rows.
ℹ Please consider using `annotate()` or provide this layer with data containing
  a single row.
All aesthetics have length 1, but the data has 2 rows.
ℹ Please consider using `annotate()` or provide this layer with data containing
  a single row.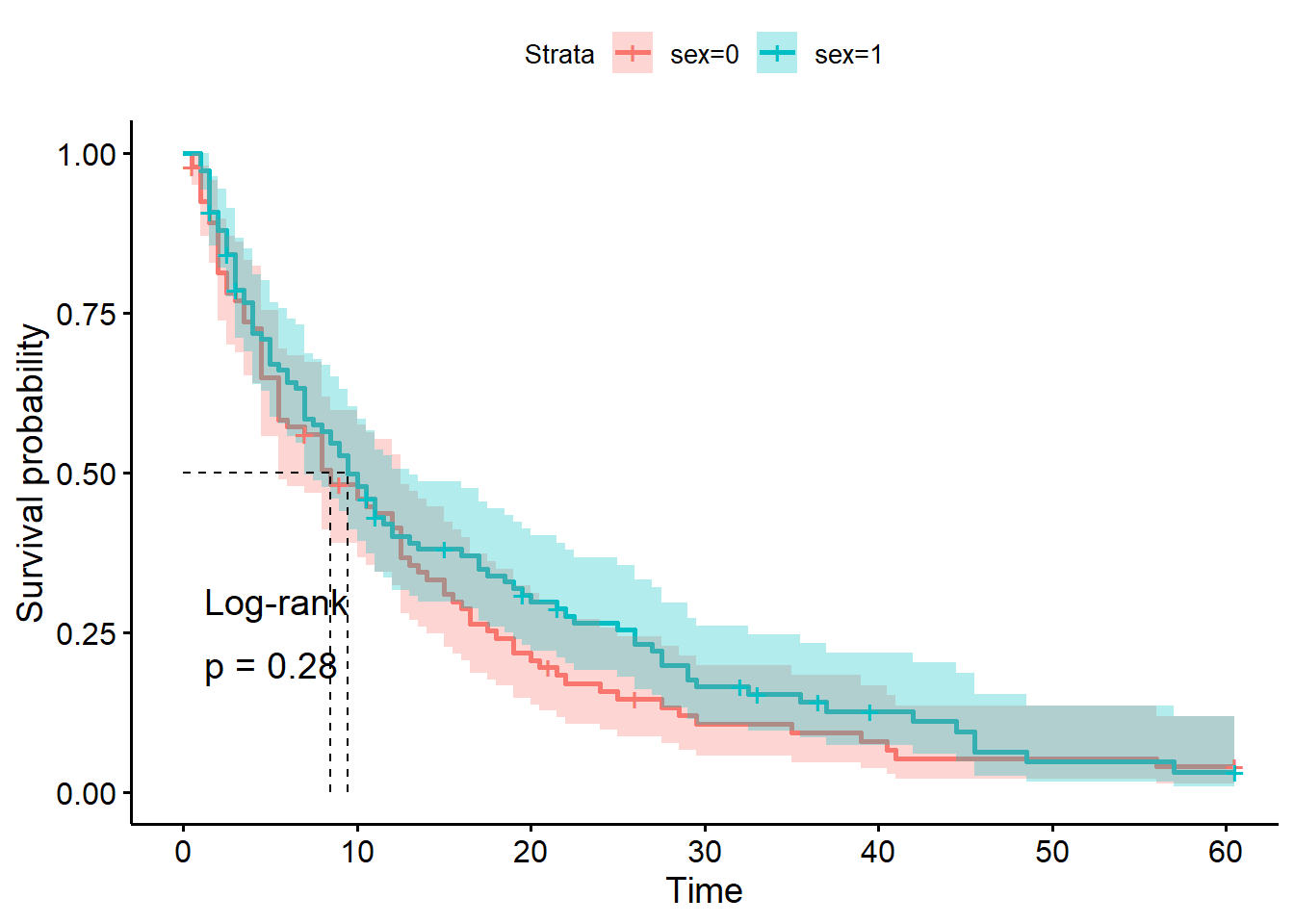

# Kaplan Meier fit for surgical data subset
fem_hosp = KaplanMeierFitter()
fem_hosp.fit(T[fem], event_observed=E[fem], label="Female patients")

<lifelines.KaplanMeierFitter:"Female patients", fitted with 92 total observations, 8 right-censored observations>

# Kaplan Meier fit for non-surgical data subset
male_hosp = KaplanMeierFitter()
male_hosp.fit(T[~fem], event_observed=E[~fem], label="Male patients")

<lifelines.KaplanMeierFitter:"Male patients", fitted with 108 total observations, 14 right-censored observations>

# Initialise a plot to capture both of the curves
plt.clf()
fig, ax = plt.subplots()

# Add the two curves, one at a time
fem_hosp.plot_survival_function(ax = ax)
male_hosp.plot_survival_function(ax = ax)

# Add the median markers for both curves
add_median_markers([fem_hosp, male_hosp], ax = ax)

# Add the p-value
pval = results.p_value
ax.text(0.6, 0.6, f"Log-rank p = {pval:.3g}", transform=ax.transAxes)

plt.show()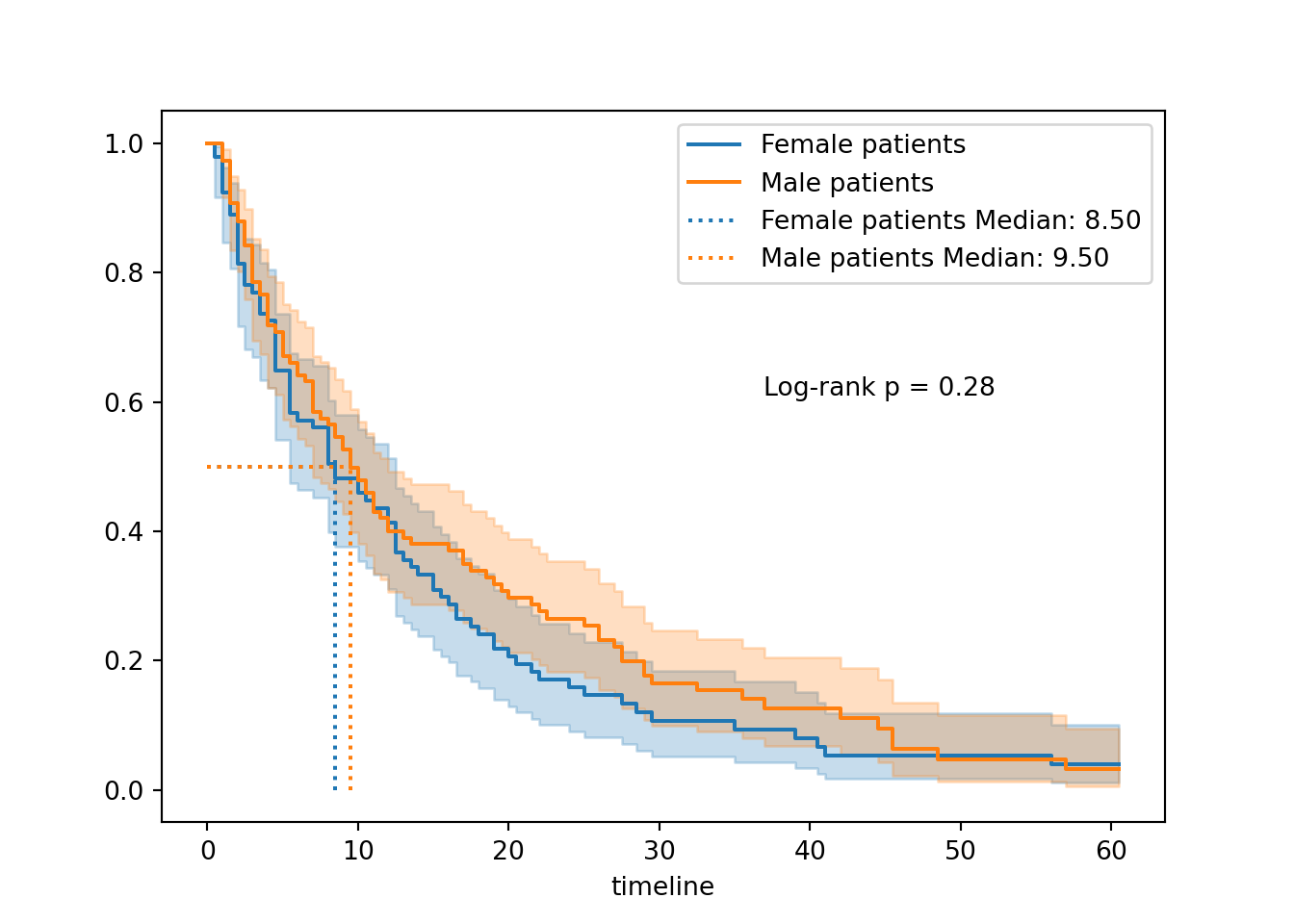

5.5 Best practices for reporting

Chances are that if you’re running a log-rank test, you’ll likely want to report it. Here are some general guidelines to follow when you do.

✓	Visualise the survival curves
	A single significance test by itself tells a reader very little. It doesn’t capture important details like sample size or direction of effect (e.g., which group is more at risk than the other). If a log-rank test is important enough to your central thesis that you’re choosing to include it in your writing, then it’s also important enough to visualise the survival curves that you compared.
✓	Comment on assumption-checking
	You don’t have to describe or show a full set of diagnostic plots in-text - that’s probably overkill (if you’re a very thorough person, you can put them in supplementary materials). But, you should at least state the assumptions of the test, the fact that you checked them, and how well you believe they are met. There are a few reasons why: Hold yourself accountable - this will make sure you do actually think about the assumptions Transparency - it helps readers determine how confident they feel in the appropriateness of your log-rank test(s) Setting a good example - researchers often follow statistical practice they learn from their peers’ publications; you have an opportunity to set a good trend!
✓	Consider the problem of multiple comparisons/false positives
	If you are doing a large number of log-rank tests, remember that the overall probability that at least one of them will give you a false positive result is higher than if you only did one log-rank test. In situations where you need to run loads of tests, consider whether correcting for multiple comparisons might be needed, to increase confidence in your conclusions.
✓	Don’t run/report log-rank tests unless they address your hypotheses
	This is maybe the most important “best practice” of them all! Never do statistical analyses for the sake of sprinkling in some extra p-values. At best, this makes your overall point less clear. At worst, it’s p-hacking. Only run tests that will actually address the research questions you had in mind when you designed the study in the first place.

5.6 Summary

The most common method for comparing two curves is known as the log rank test (or more formally, the Mantel-Cox test).

It’s analogous to a two-sample t-test in regular linear modelling. It tests the null hypothesis that, in the underlying population, the two groups have an identical survival curve.

Key Points

The null hypothesis of a log-rank test is that two groups share the same survival curve in the underlying population
A significant log-rank test means that our data are unlikely to occur by chance (but does not “prove” a difference!)
The log-rank test makes two key assumptions: independent observations and non-informative censoring
It is also a more powerful (sensitive) test when the hazards are proportional between groups